Sebelum
membaca artikel ini lebih jauh, kami harap pembaca Fisikaveritas sudah familiar
dengan persamaan Laplace, teknik iterasi dan juga pemrograman C; jika belum, kami
menganjurkan pembaca Fisikaveritas untuk membaca artikel berikut ini terlebih
dahulu:
:: Iterasi Persamaan Linier Simultan, Apakah itu?
:: Konsep Tentang Persamaan Laplace
:: Iterasi Persamaan Linier Simultan, Apakah itu?
:: Konsep Tentang Persamaan Laplace
Persamaan
Laplace 2-dimensi adalah sebagai berikut
Kita perlu melakukan diskritisasi pada suatu
persamaan diferensial jika solusi persamaan diferensial tersebut sulit dicari
solusinya secara analitik (dengan teknik integral dan/atau diferensial), dengan
melakukan diskritisasi persamaan diferensial, diharapkan kita akan mendapatkan
solusi persamaan diferensial tersebut secara numerik. Nah, maksud dari
diskritisasi persamaan diferensial sendiri sebenarnya adalah men-diskritkan
persamaan diferensial tersebut menjadi persamaan aljabar biasa sehingga solusi
persamaan diferensial tersebut dapat kita peroleh dengan teknik aljabar biasa
atau dengan teknik numerik (tambah, kurang, kali, bagi, dsb). Kita tahu bahwa
hampir semua persamaan diferensial di alam ini pada dasarnya adalah persamaan
kontinu (tidak diskrit), solusinya ada di setiap titik dan solusinya sangat
sulit didapatkan secara analitik, walaupun begitu, solusi dengan pendekatan
diskrit/numerik juga sangat memuaskan.
http://fisikaveritas.blogspot.com:
Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai
sumbernya
Mungkin Kamu
masih bingung dengan penjelasan di atas, kita langsung saja ke contoh kasus.
Sometime, learning by doing is the better way.
Sometime, learning by doing is the better way.
Kita
mempunyai suatu pelat persegi dengan ukuran 10 cm ⨯ 10 cm, di mana temperatur
pada pelat tersebut kita asumsikan steady
state (tidak berubah seiring waktu). Temperatur di sisi-sisi pelat
ditunjukkan pada gambar dan temperatur di sisi-sisi pelat tidak berubah,
besaran-besaran fisika seperti temperatur atau lainnya yang diketahui pada
sisi-sisi pelat ini disebut pula sebagai syarat batas (boundary conditions).
Nah, tujuan kita adalah mencari tahu temperatur
(T) di setiap titik pada pelat
tersebut, caranya adalah dengan mencari solusi persamaan Laplace pada pelat
kita itu.
http://fisikaveritas.blogspot.com:
Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai
sumbernya
Ada dua cara
untuk mencari solusi persamaan Laplace 2-dimensi di atas, pertama adalah dengan
cara analitik dan yang kedua adalah dengan cara numerik (diskritisasi). Sebelum
kita melangkah ke penyelesaian persamaan Laplace dengan cara numerik, kita
lihat dulu solusi persamaan Laplace secara analitik berikut untuk membandingkan
saja, dengan asumsi Kamu sudah belajar tentang cara penyelesaian persamaan
diferensial parsial dengan metode separasi variabel:
Lakukan pembagian pada persamaan di atas dengan X(x)Y(y), didapatkan
persamaan separasi variabel berikut
Dari
persamaan di atas tanpa berpanjang lebar dengan mengintegralkan persamaannya,
didapatkan bahwa
Didapatkan
solusi umum persamaan Laplace 2-dimensi sebagai berikut
Sekarang
masukkan syarat batasnya ke solusi umum di atas, maka kita dapatkan solusi
khusus berikut (solusi analitiknya)
Ahhh~ gimana?
Rumit ya, lupakan saja solusi analitiknya, tapi,
perlu Kamu ketahui bahwa jika kita berhasil mendapatkan solusi analitiknya, enaknya kita bisa mengetahui temperatur
di semua titik pada pelat tersebut, kita bisa memasukkan, katakanlah, x = 1.050 cm dan y = 4.567 cm dan kita mendapatkan temperaturnya T(1.050 , 4.567) di titik ini. Namun sayangnya, tidak semua persamaan
diferensial di alam ini dapat dicari solusi analitiknya, bahkan persamaan Laplace
pun jika geometrinya rumit, kita tidak bisa mendapatkan solusi analitiknya.
http://fisikaveritas.blogspot.com:
Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai
sumbernya
Nah kita
langsung ke pokok permasalahan, yaitu mencari solusi numerik persamaan Laplace,
kita akan mendiskritkan persamaan Laplace di atas.
Kita tahu bahwa
diferensial atau turunan pada dasarnya adalah perubahan kecil suatu kuantitas
atau besaran pada titik tertentu, definisi diferensial sendiri adalah
Nah,
diskritisasi di sini maksudnya kita melakukan pendekatan terhadap bentuk
diferensial yang kontinu di atas menjadi bentuk perubahan atau delta yang
diskrit, dengan mengambil Δx sangat
kecil. Mendiskritkan juga bermakna mendiskritkan domain sumbu-x dan sumbu-y pelat kita di atas: pertama-tama, kita akan mendiskritisasi
domain pelat, kita membuat grid (atau mesh)
serbasama pada pelat kita seperti berikut ini
Sebagai
contoh kita ambil Δx = Δy = 1 cm seperti pada gambar di atas. Jadi, ada 100
grid di dalam pelat kita, 10 untuk sumbu-x
dan 10 untuk sumbu-y. Selanjutnya,
solusi persamaan Laplace untuk temperatur akan dicari pada setiap titik simpul
grid (atau mesh) di atas.
Sekarang
kita diskritisasi persamaan Laplace-nya. kita anggap bahwa turunan pertama u terhadap x adalah sebagai berikut
Lalu, bentuk
diskrit turunan kedua dari u adalah seperti berikut
http://fisikaveritas.blogspot.com:
Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai
sumbernya
Nah,
sekarang kita sudah tahu bagaimana kira-kira mendapatkan persamaan aljabarnya ‘kan? Dari persamaan ini, kita olah
menjadi seperti berikut. Untuk memudahkan penulisan notasi, kita gunakan saja
notasi berikut ini
Jadi, kita
tulis ulang turunan kedua u:
Nah,
sekarang dengan mengambil bentuk notasi di atas, persamaan Laplace yang awalnya
berbentuk seperti ini
menjadi
seperti ini
Kita
olah-olah lagi (ingat, kita ambil Δx = Δy = 1 cm)
Akhirnya
sampai pada persamaan Laplace berbentuk seperti berikut
Untuk
memudahkan mengingat persamaan Laplace dalam bentuk seperti di atas, Kamu dapat
mengingatnya dengan stencil berikut
http://fisikaveritas.blogspot.com:
Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai
sumbernya
Untuk
iterasi kita gunakan persamaan berikut (hanya ‘dipindahruaskan’ saja)
Untuk kasus
kita u adalah temperatur (T), ganti u dengan T, maka
Persamaan di ataslah yang kemudian akan kita
iterasi, setelah kita iterasi, akan didapatkan solusinya. Lalu bagaimana
mengiterasi persamaan di atas? Caranya mudah, kita dapat menggunakan iterasi
Gauss-Seidell untuk iterasi persamaan Laplace diskrit ini. Kita tebak dulu
kira-kira berapa temperatur di semua titik simpul pada grid interior pelat,
kita tebak saja sebesar 300C; tentu saja temperatur di setiap titik
simpul pada grid interior berbeda-beda, tapi nantinya saat iterasi berlangsung,
temperatur tebakan kita ini akan terkoreksi dengan sendirinya. Nah bagaimana
proses iterasi berlangsung pada pelat dengan menggunakan persamaan di atas?
Kita lihat sedikit iterasi pada bagian ujung kiri atas pelat.
http://fisikaveritas.blogspot.com:
Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai
sumbernya
Adapun syarat batas untuk kasus kita adalah
Tebakan awal kita
Berikut
adalah gambar data temperatur pada pelat dalam bentuk grid untuk yang belum
diiterasi (iterasi ke-0)
Iterasi
pertama pada bagian di dalam kotak ujung kiri atas pelat; kita coba lakukan
perhitungan sedikit
Untuk temperatur di titik i = 1, j = 9
Untuk temperatur di titik i =
2, j = 9
Dst..
Ingat!
Iterasi Gauss-Seidell memakai hasil hitung sebelumnya.
Hasilnya
seperti berikut: gambar data temperatur pada pelat dalam bentuk grid untuk iterasi
pertama (iterasi ke-1)
Lakukan
iterasi untuk semua titik di interior, kemudian ulangi lagi iterasinya untuk
semua titik di interior tersebut.
Sampai kapan
iterasi dilakukan? Berapa kali iterasi harus dilakukan? Iterasi dilakukan terus
sampai residu atau error iterasi menjadi sedekat mungkin dengan nol, maksudnya
lakukan iterasi sampai hal di bawah ini tercapai
Saat hal di atas tercapai, artinya iterasi
yang kita lakukan telah konvergen, solusi persamaan Laplace telah didapatkan.
Kamu dapat menetapkan sendiri berapa syarat konvergensi untuk perhitungan
iterasinya, bisa saja Kamu mengiterasinya sampai residunya sebesar 0.01 atau
sebesar 0.001 lalu setelah residu itu tercapai, iterasinya Kamu sudahi.
http://fisikaveritas.blogspot.com:
Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai
sumbernya
Namun,
menghitung sendiri iterasi di atas sangatlah membosankan dan melelahkan, Kamu
dapat menggunakan komputer untuk meng-iterasi persamaan Laplace diskritnya.
Berikut kami berikan kode atau listing program C untuk menghitung iterasi
persamaan Laplace seperti di atas.
Jika Kamu tidak mau repot-repot atau tidak tahu cara meng-compile kode C program di atas, Kamu dapat langsung download programnya di sini:
Download Program Persamaan Laplace (75 kb)
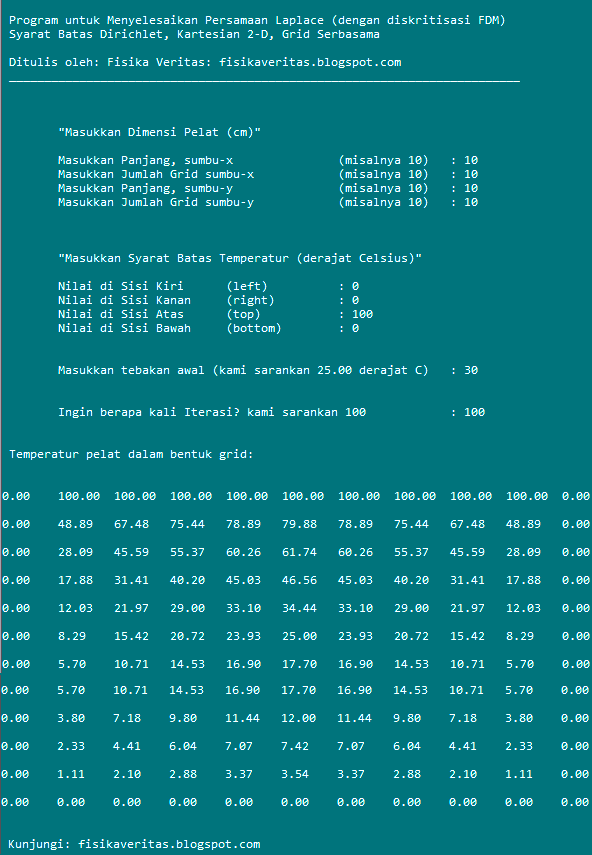
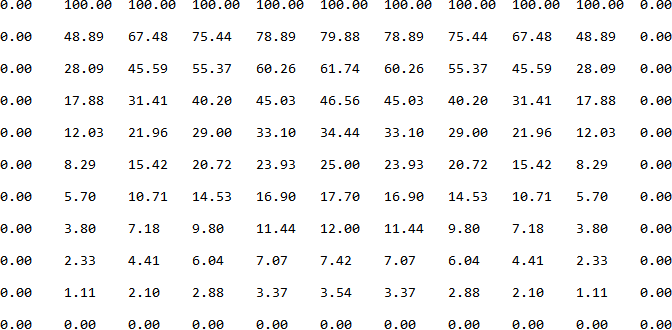
Berikut adalah hasil hitung iterasi temperatur dengan menggunakan program komputer di atas, setelah iterasi dilakukan sebanyak 100 kali.
Terlihat bahwa di sisi atas pelat temperaturnya 1000C, di sisi-sisi yang lain 00C (ini syarat-syarat batasnya), dan di dalam pelat temperaturnya seperti yang tertera pada hasil hitung di atas. Tampilan angka mungkin agak merepotkan, jadi kita plot saja hasil hitungnya dengan kontur warna seperti berikut ini:
(Baca artikel Fisika Veritas berikut untuk listing program dengan plot kontur warna yang lebih halus:
Plot Solusi persamaan Laplace 2-dimensi dengan Gnuplot)
Sebagai perbandingan, coba kita lihat bagaimana perbedaan solusi analitik yang kontinu dengan solusi numerik yang diskrit di perpotongan tengah-tengah pelat (pada garis y = 5 cm)
Jika Kamu tidak mau repot-repot meng-compile programnya, Kamu dapat mengunduh Software GUI (Graphic User Interface) Solusi Persamaan Laplace di Menu Download. Contoh tampilan software-nya seperti berikut:
Jika Kamu tidak mau repot-repot atau tidak tahu cara meng-compile kode C program di atas, Kamu dapat langsung download programnya di sini:
Download Program Persamaan Laplace (75 kb)
Berikut adalah hasil hitung iterasi temperatur dengan menggunakan program komputer di atas, setelah iterasi dilakukan sebanyak 100 kali.
Terlihat bahwa di sisi atas pelat temperaturnya 1000C, di sisi-sisi yang lain 00C (ini syarat-syarat batasnya), dan di dalam pelat temperaturnya seperti yang tertera pada hasil hitung di atas. Tampilan angka mungkin agak merepotkan, jadi kita plot saja hasil hitungnya dengan kontur warna seperti berikut ini:
(Baca artikel Fisika Veritas berikut untuk listing program dengan plot kontur warna yang lebih halus:
Plot Solusi persamaan Laplace 2-dimensi dengan Gnuplot)
Sebagai perbandingan, coba kita lihat bagaimana perbedaan solusi analitik yang kontinu dengan solusi numerik yang diskrit di perpotongan tengah-tengah pelat (pada garis y = 5 cm)
 |
| Gambar 10. Perbandingan Hasil Hitung Analitik dengan Numerik pada Garis y= 5 cm pada Pelat |
Perbedaannya
tidak terlalu jauh ‘kan?
Nah, sekarang Kamu lihat, jika kita
memecahkan persamaan Laplace secara analitik untuk kasus pelat kita di atas,
kita dapat mengetahui temperatur di semua titik pada pelat, namun kesulitannya
adalah memecahkan persamaannya. Berbeda halnya dengan memecahkan persamaan
Laplace secara numerik, kita dapat dengan mudah mencari solusinya, namun cara mendapatkan
solusinya cukup melelahkan dan membosankan jika dilakukan tanpa bantuan
komputer. Kelemahan solusi numerik adalah kita tidak bisa mengetahui temperatur
di semua titik pada pelat, kita hanya bisa mengetahui temperatur pada
titik-titik (diskrit) yang telah kita buat pada grid saja, ketelitiannya terbatas
pada seberapa kecil Δx atau Δy yang kita
ambil untuk perhitungan. Memang kita bisa saja membuat gridnya lebih kecil
(titik simpulnya lebih banyak) agar perhitungan lebih teliti, namun
perhitungannya akan lebih banyak memakan waktu.
http://fisikaveritas.blogspot.com:
Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai
sumbernya
Orang-orang
lebih menyukai memecahkan suatu persamaan diferensial secara numerik (dengan
bantuan komputer) dibandingkan memecahkan suatu persamaan diferensial secara
analitik, walaupun sebenarnya orang-orang lebih menyukai solusi analitik jika
solusinya tersedia; perlu kita ketahui bahwa hanya sedikit sekali persamaan
diferensial pada kasus nyata di dunia ini yang sudah ditemukan solusi
analitiknya.
Memecahkan
persamaan diferensial dengan cara numerik diaplikasikan secara luas pada dunia modeling/simulasi dan juga rendering dengan komputer.
Jika Kamu tidak mau repot-repot meng-compile programnya, Kamu dapat mengunduh Software GUI (Graphic User Interface) Solusi Persamaan Laplace di Menu Download. Contoh tampilan software-nya seperti berikut:
 |
| Gambar 11. Contoh Tampilan Software GUI Solusi Persamaan Laplace dari Fisika Veritas |
Sumber bacaan terkait yang lebih formal:
- Boas, Mary L., Mathematical Methods in the Physical Sciences, Second Edition. John Wiley & Sons Inc., 1983
- Hirsch, Charles, Numerical Computation of Internal and External Flows, Second Edition, John Wiley & Sons, Ltd., 2007
- Spiegel, Murray R. 1971. Theory and Problems of Calculus of Finite Differences and Difference Equations. McGraw-Hill, Inc. USA
http://fisikaveritas.blogspot.com:
Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai
sumbernya
Trivia:
- Solusi analitik biasanya berbentuk fungsi (analitik), sedangkan solusi numerik biasanya berbentuk angka saja (numerik).
- Metode diskritisasi yang digunakan pada artikel ini adalah metode beda hingga (finite difference method / FDM) yang mana metode ini mengaplikasikan deret Taylor langsung pada definisi diferensial. Skema diskritisasi implisit.
- Pada turunan pertama u, kita menggunakan pendekatan yang dinamakan first order forward difference, kita memakai deret Taylor orde-1. Sedangkan pada turunan kedua u, kita menggunakan pendekatan central difference.
- Pendekatan untuk turunan pertama dan turunan kedua dapat pula ditulis seperti di bawah ini












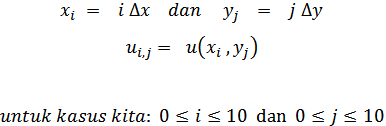
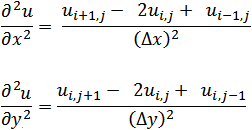
















Sangat membantu..
ReplyDeleteTerima kasih banyak yaa...
Terima Kasih, sangat bagus dan mudah dipahami, Semoga UAS saya lancar (-_-)
ReplyDelete