Fisika Veritas: Diskritisasi dan Listing Program C untuk Heat Equation 2-Dimensi

Sebelum lebih jauh membahas tentang heat equation, bagi pembaca yang kurang familiar dengan diskritisasi maupun teknik iterasi, kami sarankan untuk baca terlebih dahulu tentang

http://fisikaveritas.blogspot.com: Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai sumbernya

Heat equation atau persamaan difusi adalah persamaan yang menggambarkan atau mengatur peristiwa difusi suatu kuantitas fisis (u); kuantitas fisis (u) ini bisa berupa temperatur, tekanan, dan lain sebagainya. Heat equation, tidak seperti persamaan Laplace, ia menggambarkan perubahan suatu kuantitas fisis terhadap waktu. Heat equation juga menggambarkan difusi/penyebaran suatu kuantitas fisis.

Gambar berikut dapat membantu memahami perbedaan persamaan Laplace dengan heat equation.

Gambar 1. Perbandingan Persamaan Laplace dengan Heat Equation

Untuk menghitung solusi heat equation, perlu diketahui syarat batas (nilai di batas-batas atau ujung-ujung sistem) dan juga syarat awal (nilai awal di seluruh sistem).

Heat equation secara matematis ditulis seperti berikut (lihat penurunan rumusnya di sini)

Dalam koordinat kartesian 2-Dimensi ditulis

Pada heat equation di atas, α adalah konstanta difusivitas termal bahan (satuannya m²/s).

Besaran fisis u berubah terhadap waktu (t) dan berubah terhadap ruang (x, y). Jadi, u adalah fungsi dari x, y, dan t. Ditulis secara matematis

Untuk mendiskritisasi heat equation 2-D di atas, kita gunakan metode yang sama seperti metode yang digunakan pada diskritisasi persamaan Laplace, artikel Fisika Veritas sebelumnya.

Untuk memudahkan penulisan notasi, kita gunakan notasi berikut ini

Dengan subskrip i dan j berturut-turut menyatakan fungsi terhadap x dan y, sedangkan k adalah time step yang menyatakan fungsi terhadap t; semuanya secara diskrit.

Untuk mendiskritisasi persamaan diferensial di atas, perlu diambil bentuk infinitesimal dx, dy, dt berturut-turut sebagai bentuk finitesimal Δx, Δy, dan Δt yang kecil. (Sebenarnya menggunakan deret Taylor)

Kita tulis ulang heat equation dalam bentuk diskrit

Untuk memudahkan, kita ambil Δx = Δy, diperoleh bentuk diskrit yang siap digunakan pada kode komputer atau listing program untuk melakukan simulasi suatu perambatan panas atau lainnya seperti berikut ini

Dengan

Untuk ‘mengingat’ persamaan diskrit di atas, dapat digunakan stencil berikut ini

Gambar 2. Stencil pada Heat Equation Diskrit

Tidak seperti diskritisasi persamaan Laplace di artikel sebelumnya, diskritisasi heat equation di atas berskema eksplisit, maksudnya, nilai u^k+1_i,jpadapersamaan di atas dapat langsung dihitung karena nilai-nilai pada ruas sebelah kanan sudah diketahui dari syarat awal (untuk k = 0). Karena kita memakai skema eksplisit untuk menghitung solusi heat equation, perlu dipatuhi syarat stabilitas berikut ini (tidak perlu kita buktikan di sini)

Karena Δx = Δy, syarat kestabilannya menjadi

Syarat stabilitas di sini maksudnya, jika kita pilih Δt yang tidak memenuhi kriteria stabilitas di atas, maka perhitungan nilai u pada setiap kenaikan time step k akan memperbesar error hitung dan hasil hitung yang didapatkan menjadi tidak benar atau tidak stabil.

http://fisikaveritas.blogspot.com: Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai sumbernya

Kita masuk ke contoh kasus untuk mengaplikasikan persamaan diskrit dari heat equation yang telah kita dapatkan sebelumnya.

Sebuah pelat aluminium (α = 0,00008418 m²/s) berbentuk persegi (2-D) dengan panjang sisi-sisinya adalah 5 meter. Pada awalnya pelat bertemperatur 0⁰C di setiap titik pada pelat tersebut. Kemudian secara tiba-tiba salah satu sisi pelat tersebut diberi temperatur tetap 100⁰C, sedangkan sisi-sisi lainnya dijaga tetap bertemperatur 0⁰C. Bagaimanakah kontur temperatur di dalam pelat tersebut seiring waktu? Buat grid pada pelat tersebut dengan Δx = Δy = 1 meter.

Gambar 3. Syarat Batas dan Awal serta Grid Pelat

Temperatur pada pelat itu pada mulanya 0⁰C pada semua titik di pelat, karena salah satu sisi diberi temperatur tetap sebesar 100⁰C, maka temperatur pada pelat akan berubah seiring waktu. Kita akan mencoba menghitung perubahan atau perambatan temperatur di pelat tersebut seiring waktu.

Kita gunakan persamaan berikut ini untuk menghitung temperatur (u)

Konstanta difusivitas (α ) aluminium adalah sebesar 0,00008418 m²/s.

Syarat Batas (Boundary Conditions):

Syarat Awal (Initial Conditions):

Syarat stabilitas

Untuk kasus kita, syarat stabilitasnya adalah

Kita ambil syarat stabilitas Δt = 2969.8 detik

Berarti untuk setiap kenaikan k, maka kondisi pelat yang akan kita amati temperaturnya adalah kelipatan 2969,8 detik setelah salah satu sisi pelat diberi temperatur konstan sebesar 100⁰C. Jadi pada time step k = 1, t = 2969.8 detik; pada time step k = 2, t = 5939.6 detik; dst.

Kita coba sedikit melakukan perhitungannya secara manual seperti berikut ini

Pada k = 1, atau t =2969.8 detik

Untuk i = 1 dan j = 4

Untuk i = 2 dan j = 4

Dan seterusnya, lakukan perhitungan sampai k yang diinginkan untuk semua i dan j pada pelat.

Adapun melakukan perhitungan di atas secara manual (dengan tangan) sangatlah melelahkan dan tidak efisien, program komputer dapat melakukan perhitungan di atas dengan cepat, tepat, dan mudah. Listing program C untuk menghitung perambatan temperatur pada pelat persegi (2-D) telah kami sajikan di bawah ini dan dapat dimodifikasi sesuai dengan kasus yang bersangkutan.

/*  Fisika Veritas , kunjungi : fisikaveritas.blogspot.com  */
#include "stdio.h"
#include "conio.h"

main()
{

 int i, j, m, n, x, N, BSTEP;
 float T[20][20][20], l, r, t, b, tawal, dt, alfa, dx, Detik;

 printf("\n Program untuk Menyelesaikan Persamaan Difusi (dengan diskritisasi FDM)\n");
 printf(" Syarat Batas Dirichlet, Kartesian 2-D\n");
 printf("\n Ditulis oleh: Fisika Veritas: fisikaveritas.blogspot.com\n");
 printf(" _________________________________________________________________________\n\n\n");


/* Bentuk: Pelat Persegi Panjang */
printf("\n\t\"Masukkan Dimensi Pelat Persegi\"\n\n");
printf("\tMasukkan Panjang Sisi (misalnya 5)      :    meter\b\b\b\b\b\b\b\b"); scanf("%d",&x);
printf("\tMasukkan Jumlah Grid setiap sumbu (misalnya 5): ");        scanf("%d",&m);

/* Syarat Batas*/
printf("\n\n\n\t\"Masukkan Syarat Batas Temperatur (derajat Celsius)\"\n\n");
printf("\tNilai di Sisi Kiri    (left)     : ");   scanf("%f",&l);
printf("\tNilai di Sisi Kanan  (right)  : ");  scanf("%f",&r);
printf("\tNilai di Sisi Atas    (top)  : ");  scanf("%f",&t);
printf("\tNilai di Sisi Bawah  (bottom) : ");  scanf("%f",&b);

/* Temperatur Pelat pada Awalnya (Syarat Awal) */
printf("\n\n\tMasukkan Temperatur Awal Pelat (derajat Celsius) : "); scanf("%f",&tawal);

/* Konstanta Difusi Termis (alfa) */
printf("\n\n\tKonstanta Difusi Termis Alumunium     0.00008418  m2/s");
printf("\n\tKonstanta Difusi Termis Emas      0.000127    m2/s");
printf("\n\tKonstanta Difusi Termis Besi      0.000023    m2/s");
printf("\n\tKonstanta Difusi Termis Perak      0.0001656   m2/s");
printf("\n\tKonstanta Difusi Termis Baja 1\% Karbon 0.00001172  m2/s");
printf("\n\n\tMasukkan Konstanta Difusi Termis (alfa):          m2/s\b\b\b\b\b\b\b\b\b\b\b\b\b\b"); scanf("%f",&alfa);

/* Besar Time Step dan Banyaknya Time Step */
printf("\n\n\tMasukkan Banyaknya Time Step (Coba 5)  : "); scanf("%d",&BSTEP);
 /* Besarnya Time Step dt Mengikuti Syarat Stabilitas */
 dx = x/m;
 dt = ((dx*dx)/(4*alfa));

m++;
n=m;
n++;
        
 /* Mulai Definisi Syarat Batas */
 for(N=0; N<=BSTEP-1; N++)
 {
  for(i=1; i<=m; i++)
  {
   T[i][1][N]=b;
   T[i][n][N]=t;
  }
 }
       
 for(N=0; N<=BSTEP-1; N++)
 {
  for(i=1; i<=n; i++)
  {
   T[1][i][N]=l;
   T[m][i][N]=r;
  }
 }
 /* Selesai Definisi Syarat Batas */

  /* Syarat Awal : Temperatur Awal Pelat pada Nilai Interior) */
 for(i=2; i<=m-1; i++)
 for(j=2; j<=n-1; j++)
  T[i][j][0]=tawal;
 
 /* Perhitungan Skema Eksplisit
 Diskritisasi persamaan Difusi */
 for(N=0; N<=BSTEP-1; N++)
 {
  for(i=2; i<=m-1; i++)
        {
   for(j=2; j<=n-1; j++)
            {
    /* Persamaan Difusi Diskrit */
    T[i][j][N+1] = ((alfa*dt/(dx*dx))*(T[i+1][j][N] + T[i-1][j][N] + T[i][j+1][N] + T[i][j-1][N] - (4*T[i][j][N]))) + T[i][j][N];
            }
        }
 }
            
 
 /* Menampilkan hasil hitung iterasi dalam (bentuk) grid pelat persegi panjang */
 printf("\n\n Hasil hitung dalam bentuk grid: \n\n\n");
 for(N=0; N<=BSTEP-1; N++)
 {
  Detik = dt*N;
  printf("\n Detik ke  %.4f \n\n", Detik);
  for(j=n; j>=1; j--)
  {
   for(i=1; i<=m; i++)
   {
    printf("%.2f\t", T[i][j][N]);
   }
   printf("\n");
  }
  printf("\n");
 }

 printf("\n Kunjungi: fisikaveritas.blogspot.com");         

  getch();
}

http://fisikaveritas.blogspot.com: Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai sumbernya

Jika Kamu tidak tahu cara meng-compile listing program C di atas, kamu dapat langsung download programnya di sini.

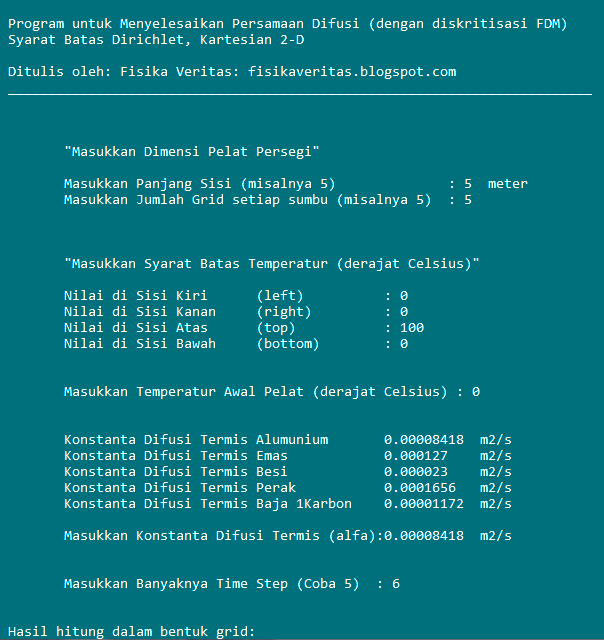
Download Program Heat Equation (37 kb)

Contoh tampilan programnya adalah seperti berikut untuk contoh kasus pelat persegi kita di atas

Hasil yang didapatkan dengan program di atas adalah matriks yang berisi data temperatur (dalam derajat Celsius) pada grid pelat di setiap time step. Kita susun seperti berikut

Gambar 5. Matriks Temperatur pada Pelat

Karena tampilan angka mungkin kurang menarik, kita plot angka tadi ke dalam kontur warna temperatur pelat seperti berikut ini

Gambar 6. Kontur Temperatur (sudah diperhalus) pada Pelat

Gambar 7. Kontur Temperatur pada Pelat Seiring Waktu

Semoga bermanfaat.

http://fisikaveritas.blogspot.com: Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai sumbernya

TRIVIA:

Heat equation adalah salah satu prototipe persamaan parabolik; persamaan Laplace dan persamaan Poisson merupakan prototipe persamaan eliptik; sedangkan persamaan gelombang merupakan prototipe persamaan hiperbolik. Nama-nama ini muncul berdasarkan bentuk umum persamaan diferensialnya yang mirip dengan potongan kerucut (conic section).

Dasar-dasar modeling dan simulasi komputer adalah menghitung solusi persamaan-persamaan diferensial parsial seperti yang kita lakukan tadi. Perhitungan yang melibatkan kerumitan geometri, kerumitan syarat-syarat batas, syarat-syarat awal, dan metode diskritisasi membutuhkan daya komputasi yang tinggi. Metode diskritisasi yang dipakai di sini adalah metode beda hingga (finite difference method) yang menerapkan deret Taylor pada definisi diferensial. Ada banyak metode diskritisasi untuk menyelesaikan persamaan diferensial parsial selain metode beda hingga, di antaranya yang terkenal di kalangan industri dan penelitian adalah metode elemen hingga (finite element method).

http://fisikaveritas.blogspot.com: Diizinkan menyalin artikel ini jika mencantumkan FISIKAVERITAS sebagai sumbernya

:: Diskritisasi dan Listing Program C (+Gnuplot) Heat Equation 1-D dengan Syarat Batas Neumann

Fisika Veritas

Laman

Diskritisasi dan Listing Program C untuk Heat Equation 2-Dimensi

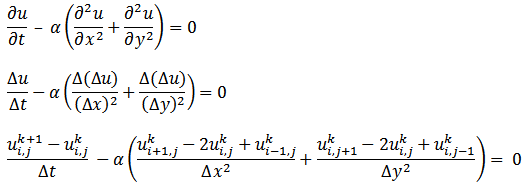
No comments :

Post a Comment